SUDOKU
Sudoku rules
Plan of sudoku puzzle game consists of 9 x 9 squares that are divided into 9 boxes marked with bold lines. At the start some of the squares are filled with numbers from 1 to 9. It is necessary to fill the remaining squares of the puzzle with numbers from 1 to 9 in such a way that the following conditions are met:- Each row of the puzzle can contain each number from 1 to 9 only once
- Each column of the puzzle can contain each number from 1 to 9 only once
- Each box of the puzzle can contain each number from 1 to 9 only once
Sudoku for everybody
We have prepared for you different levels of difficulty so that the puzzle can be enjoyed by beginners, advanced users as well as real sudoku experts.- Easy sudoku
- suitable for those who are only starting with sudoku or do not wish to exercise their brains too much.
- Medium sudoku
- suitable for advanced users
- Difficult sudoku
- for all those who want to exercise their brains
- Very difficult sudoku
- these puzzles can be solved only by true sudoku experts
How to solve sudoku
For those who are only starting with sudoku we are going to show some techniques on how to solve sudoku puzzles. Some of them are easier and some of them are more complicated.
The only possible number
This technique is the easiest and the most commonly used technique of solving sudoku. It is about determinig the number that can be placed in a given square. We are using an elimination technique. We determine which numbers can not be in the given puzzle square because they already appear in the given box, row or column. When there is only one number left that can be placed in the given square, we can write it there.
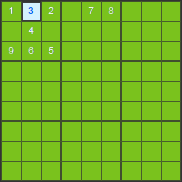
We will show this technique on the following example. Our objective is to find out which number can be placed in the first row and first column of the puzzle.
number 1 - not possible, it already appears in the given row and column, number 2 - not possible, it already appears in the given row and box, number 3 - not possible, it already appears in the given box, number 4 - not possible, it already appears in the given row, number 5 - not possible, it already appears in the given column, number 6 - not possible, it already appears in the given box, number 7 - not possible, it already appears in the given row and also given box, number 8 - possible, number 9 - not possible, it already appears in the given row
We are left with only one possible number that can be placed in the first square and that is number 8.
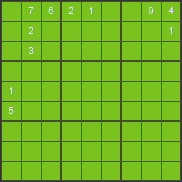
One possible placement
In case that we can not find the right number using the previous technique, this algorithm often helps. With this technique we are looking for a square in the given box, row or column where we can place a given number.
We can show this technique on the following example. We will look for a square in the first box of the puzzle where we can place number 1.

We can also use the same rule of puzzle solving when looking for one possible placement for a number within a given row or column.
By using of these two techniques it is possible to resolve a great amount of puzzles. On our sudoku site you can resolve all easy sudoku with these steps.
Techniques with several squares at the same time
When solving sudoku in previous algorithms we worked only with one square for which we determined a possible number. Or more precisely, we worked with a single number for which we wanted to find a suitable square. However, it is not possible to resolve all the puzzles only with using previous techniques. Sometimes it is necessary to take into consideration more squares at the same time.
We will show this technique for puzzle solving on an example. We will determine the placement of numbers in the first box.
In the first box numbers that are missing are 3, 7 and 8. Number 3 can be in any square. Number 7 can not be in the first row because it already appears there. So it can only be in the yellow or green square. Similarly, number 8 can only be in the green or yellow square. The yellow and green square will then contain numbers 7 and 8. We do not know yet which one will appear in which square but certainly these numbers will appear in both squares. Number 3 can not be then in the yellow or green square because in that case either number 7 or 8 would not fit in. For number 3 there is only one possible placement left - the white square.


We showed you a rather simple example of puzzle solving when considering several squares at the same time. Similarly, it is necessary to consider several squares within a row or column.
Trial - error techniques
When everything else fails, there is only one option left of how to resolve the puzzle sudoku. It is necessary to have a guess of a number in a square and in case we arrive to a wrong scenario, it is necessary to go back to the square with an estimated number. When using this technique it is good to have a guess of a number in the square with less possible options or in the square that is expected to reveal a wrong scenario soon.
On this sudoku site, this technique is necessary to use only in the category of very difficult sudoku.
We wish you a lot of fun at solving sudoku puzzles.
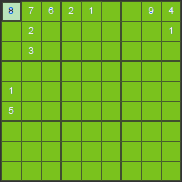 After eliminating all other possibilities it is obvious that the square in 1st row and 1st column must contain number 8.
After eliminating all other possibilities it is obvious that the square in 1st row and 1st column must contain number 8.
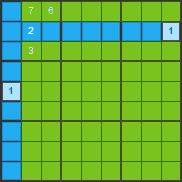 We will eliminate the placements where we can not put number 1
We will eliminate the placements where we can not put number 1
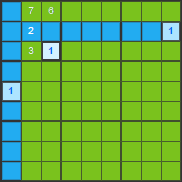 Regarding number 1 in the first box, the only possible placement left is in 3rd row and 3rd column
Regarding number 1 in the first box, the only possible placement left is in 3rd row and 3rd column
 For number 3 there is only one possible placement left - the white square. Therefore we can write it there.
For number 3 there is only one possible placement left - the white square. Therefore we can write it there.